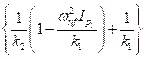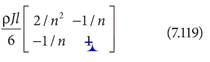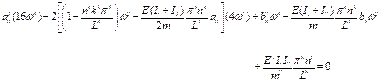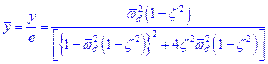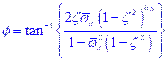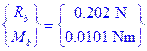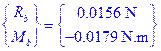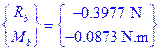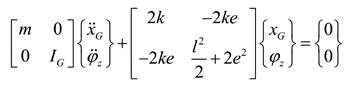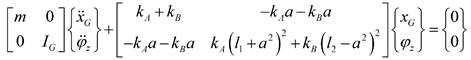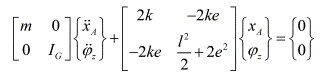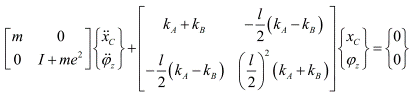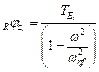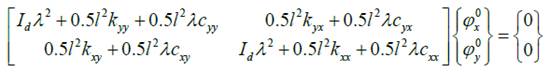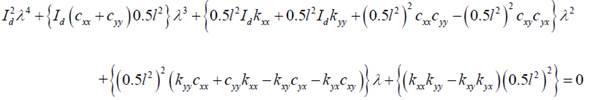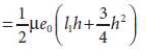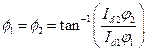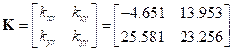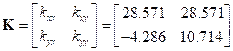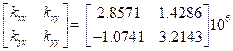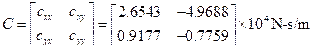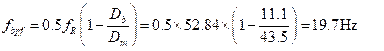Rotor Systems: Analysis and Identification

(Errata and Answers to Selected Exercise Problems)

Errata in “Rotor Systems: Analysis and Identification, CC Press, Boca Raton, USA” Authored Rajiv Tiwari

(please report if you find more: rtiwari@iitg.ac.in)

S.N.		Page		Specific location	Correction/inclusion
Preface		xvii		List of Ph D students helped	Rajeswara Rao Bhyri		✔
Ch02		22		Section 2.1	“p” is missing In I = p d^4/64		✔
		31		Example 2.1	of 98.1 112.5 kN/m. should be “88.45-112.50 kN/m”
		40			Herein, the moment is taken with respect to the C, the moment can also be taken about G. In that case moment equation will contain x and y along with theta. But since Eqns. (a) and (b) contain theta we need to solve all three equations simultaneously. In chapter 11 the moment was taken about the G to get EOM in theta direction (page 671, Eqn. c).
		49		2.5	The angle, f, represents the phase between the force and the radial response. Add “The initial phase of the unbalance is considered as zero.”
		69		Exercise 2.1	Show that it occurs always at frequency ratio of less than one.		✔
		76		Exercise 2.25xx	For a cantilever shaft with a thin disc at the free end, if the transverse and torsional natural frequencies are the same, then the ratio of the length of the shaft to the diameter of the disc would be (take Poisson’s ratio as 1/3 for the shaft material) (a) (b) (c) (d)
Ch04		162		Equation 4.52			✔
		178-179		Exercise 4.8	All jz should be jx.
		182		Exercise 4.20
Ch05		204		Eqn. 5.5	Only negative sign is valid for negative m .
		216		Fig. 5.29	In the figure “replace Ip with Id”
		240		Exercise 5.4	‘+” is missing after		✔
		240		Exercise 5.5	Change initial tilt j to j0.
		240		Exercise 5.6	“supported freely” to be replaced by “simply supported” Delete whole last line “For the cylinder .”
		241		Exercise 5.7	A shaft of total length l on the end bearings carries two discs a disc at the quarter-length points. The discs have disc has mass … to be modified as
		241		Exercise 5.8	kt = 2000 N-m/ rad		✔
		241		Exercise 5.8	Exercise 5.8 Obtain the forward and backward transverse critical speeds of the rotor system shown in Figure 5.48. Take the shaft as rigid. It is assumed that it oscillates (processes) about its centre of gravity while whirling (i.e., pure tilting without translational motion). The effective torsional stiffness of the bearings is N-m/rad, the polar and diametral mass moment of inertia of the rotor are 0.03 kg-m^2 and 0.2 kg-m2, respectively. Consider the gyroscopic effects. Delete last two but one lines? Not required?
		241		Exercise 5.8	Delete the following sentence :Bearing support distance is 1 m and center of gravity of the rotor is 30 cm from the right support bearing.”		✔
		242		Exercise 5.13	1. Add at the end of first line “of a cantilever rotor system” 2. to be modified as
		242		Exercise 5.14	“The shaft modulus of rigidity of the shaft …”
		243		Exercise 5.18	Fig. 5.51: change shaft lengths a and b instead of l and 2l.
		244		Exercise 5.23	In seventh line “Ip = 0.1 kg-m^2”
		244		Exercise 5.24	Remove damping matrix:
		245		Exercise 5.29	“Obtain the forward and backward transverse critical speeds corresponding …”
		246		Exercise 5.30	Change: kb = 1 kN/...k = 10 kN/m
		247		Exercise 5.33	Delete as indicated
		249		Exercise 5.35xviii	Then first forward natural frequency as compared to without gyroscopic effect would
Ch06		293		Eqn. (i)	Correct the first row second column as:
		327		Exercise 6.10	(Shaft A and arm have opposite motion)
		328		Exercise 6.11	…are kg-m^2 and kg-m^2, respectively. (change is in second part )
		329		Exercise 6.17	“cm” missing in the end “16 cm”
		331		Exercise 6.21	Delete: IpF = 0.006 kg-m^2.
		331		Exercise 6.21	Units “kg-m^2“ missing in second and third lines for Ip
		332		Exercise 6.25	Given data (assumed) and from it we have =0.1 m; = 0.3 m; = 0.1 kg-m^2; = 0.02 kg-m^2; =0.04 kg-m^2; = 0.3 kg-m^2; N-m/rad; N-m/rad ; and N-m/rad
Ch07		352		Eqn. (h)	(page322.pdf file attached)
		360		Equation 7.99			✔
		374		subscripts
		375			write ‘2’ in second diagonal term instead of 1
		377		Example 7.8	Eqns. (c) and (d): in extreme right vector “n” to be replaced by “2”. Also in line below Eqn. (d).
		378		Example 7.8	Make changes ; ; .
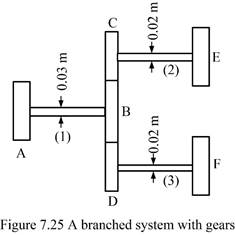
		378		Example 7.9	Figure 7.25 need to be replace (its diameters are dAB = 0.03 m, dCE = 0.02 m, and dDF = 0.02 m.)
		384		Exercise 7.9	Add “Speed of shaft A is 600 rpm and of the arm is 300 rpm with opposite sense of rotation.”
		384		Exercise 7.10
		385		Example 7.12: last line	cm, cm, cm, and cm
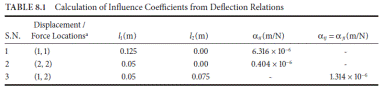
Ch08		400		Example 8.3	Table 8.1 shows the systematic calculation of influence coefficients for above expressions. Influence coefficients have been obtained by substituting l1 = 0.05 m and l2 = 0.075 m in above expressions. Delete 3^rd and 4^th columns
		402		Example 8.4	Line 3: H4 should be D4
		408		Eqn. 8-37	[F^*]
		447		Terms missing
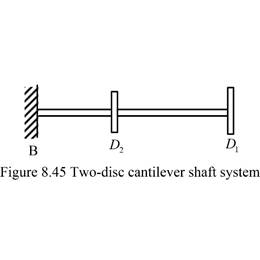
		449		Figure 8.45	Free end disc D1
		450		Example 8.12	Update as per solution as per calculation EIl instead of EIl^3 ... Hence, EIl^3 =450.89 742.20 N-m^3. Update Table 8.13
		452		Exercise 8.4	Add in the end “Take E = 2.1 x 10^11 N/m^2.”
		452		Exercise 8.7	o All disc diameter to be capital D (same for all other examples?) o Add: For a Jeffcott rotor with an offset disc, the following influence coefficients are valid (Refer Table A.1-7 for Deflection relations in terms of z)
		454		Exercise 8.8, Line 4	Shaft segments, of diameter 0.01 m, have the Make disc diameters as D1, D2, … “take diameter of discs as cm, cm, and cm”
		454		Exercise 8.9	“The masses of discs are m1 = 5 kg, m2 = 2 kg,” The diametral mass moments of inertia of the discs …
		455		Exercise 8.12	The mass of the of thin discs are
		456		Exercise 8.16, Line 7	…m4 = 7 kg, and m5 = 8 kg.
		457		Exercise 8.17	1. Consider the rotor system shown in Figure 8.63 for obtaining the transverse natural frequency 2. A thin disc, of mass 3 kg and diametral mass moment of inertia 0.01 kg-m^2, is …
				Exercise 8.18	1. Consider the rotor system shown in Figure 8.63 for obtaining the transverse natural frequency 2. A thin disc, of mass 3 kg and diametral mass moment of inertia 0.01 kg-m^2, is …
		458		Exercise 8.21	Exercise 8.21 Obtain the natural frequencies of the rotor system shown in Figure 8.66. Assume the rotor has free–free boundary conditions. Take the shaft material Young’s modulus as E = 2.1 × 1011 N/m2. The transverse stiffness of each bearing is k = 200 N/mm, The mass of the rotor is 15 kg, and the polar and diametral mass moments of inertia of the disc are 0.3 kg-m2 and 0.2 kg-m2, respectively. Neglect the shaft mass and gyroscopic effects. Use the TMM
		458		Exercise 8.23			ignore
		459		Exercise 8.27	Delete from the end “and the diametrical mass moment of inertia of the disc”
		462		subscript	??
		462			add formula for simply supported beam with a moment at some location. https://www.engineeringtoolbox.com/beams-fixed-both-ends-support-loads-deflection-d_809.html
					Exercise 9.10 (cantilever two disc cases) Try to uniformalise In Exercise 9.8 Take D1D2 = 50 mm (as per figure) In Exercise 8.9 Take D1D2 = 75 mm and m1 = 2 kg and m2 = 5 kg (as per Examples 8.3, 8.7 and 8.11) In Example 8.11 Take left disc as D2 (in figure) m1 (5 kg) > m2 (2 kg) 9.2/9.10/8.2 are similar problems (in 9,10 take D1D2 = 50 mm?)
Ch09		468		Fig. 9.1 subscript	Change all and f(z, t)
		492		[Nf]	NF1 is multiplication of first two terms in brackets
		499		Eqn. (g)
		499		Eqn. (h)
		503		Example 9.3	following natural frequencies of the system rad/s, and rad/
		527		Example 9.9 (spelling of Rayleigh’s)	For Example 9.2 obtain the Rayleigh’s damping coefficients
		508		Fig. 9.20 (Example 9.5)	Mass at node 2 is 1 kg; also below Fig. 9.20 “m2 = 1 kg”
		530		Example 9.10 (in the end)	which gives natural frequencies as 14.24 rad/s; 58.72 rad/s On comparison with Example 9.2 (14.24 rad/s; 57.57 rad/s), with the same number of elements, it could be seen that not much difference in the determined fundamental natural frequency even with the condensations of some of DOFs. However, now the size of the matrix has decreased drastically from 6×6 to 2×2. For more number of elements it is expected that other higher natural frequencies estimation would be improved.
	538		Exercise		(Assume the mass density, r = 7800 kg/m^3 of shaft material)
	538		Exercise 9.2		Add in the end “The shaft is made of steel with 2.1 x 10^11 N/m^2 as Young’s modulus, E, and 7800 kg/m^2 as the mass density, ρ.”
	539		Exercise 9.8		Assume the mass density, r = 7800 kg/m^3 of shaft material
	540		Exercise 9.10		change in fig. distance between two discs 0.75 m)
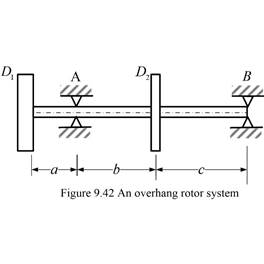
	540		Exercise 9.12		b = c = 0.7 m Draw Fig. 9.42 proportionately
	542		Exercise 9.14, second line		simply supported end conditions
Ch11
	613		Example 11.2		A rigid rotor of mass 5 kg
	614		Table 11.2		= 5.9175×10^10 ; = 3.3750×10^14; = 7.4600×10^12 Correct in 3Row 2Column as: (a3 a2 - a4 a1) = 5.9113×10^10 = 3.3750×10^14
	624		Equation 11.47			✔
	633		Example 11.7		Correction in moment of area formulae (correct all numbers accordingly) Solution: The stiffness of the shaft in two principal directions are given as N/m with m^4 and N/m with m^4 Now, we have rad/s and rad/s Hence, the rotor will be unstable in speed range 42.47 rad/s to 47.19 rad/s due to shaft asymmetry and also in speed range of 21.23 to 23.59 rad/s due to unbalance.
	644		Eqn. 11.114		Replace l with L
	645		Between Eqn. 11.118 and to 11.119 (first term )		which can be rearranged to
	645		Between Eqn. 11.119 up to 11.121		Replace l with L
	667		Equation 11.221		negative sign is giving -negative imaginary part so not a physical solution? since square of natural frequency cannot be negative?
	671				Herein, the moment is taken with respect to the G, the moment can also be taken about C. In that case moment equation will contain only theta. But since Eqns. (a) and (b) contain theta we still need to solve all three equations simultaneously. In chapter 2 the moment was taken about the C to get EOM in theta direction (Eqn. 2.44), page 40).
	675		Exercise 11.2		Shift this to Exercise of chapter 10
	676		Exercise 11.2		Add at the end “(i) Consider only stiffness direct and cross-coupled linear coefficients. (ii) Consider both stiffness and damping direct and cross-coupled linear coefficients.”
	667		Exercise 11.8viii		11.8 (viii) A rotor-bearing system has the following properties: rotor mass, m = 1 kg, equivalent bearing stiffness and damping coefficients of both bearings are kxx = kyy = 10 kN/m, kxy = 10 kN/m, kyx = 1 kN/m, cxx = cyy = 10 kN-sec/m, cxy = 10 kN-sec/m, cyx = 0.1 kN-sec/m
	678		Exercise 11.8xxiii		A Jeffcott rotor with an elliptical cross-section shaft (with semi-major axis a = 6 cm and semi-minor axis b = 4 cm). The second moment of areas about two principal axes are given as pab^3/4 and pa^3b/4. The disc mass is 20 kg, the shaft span l = 1 m and Young’s modulus E = 2.1´10^11N/m^2. The instability zones in the rotor system due to unbalance excitation would be within the speed range of (in rad/s) (A) 156 – 215 (B) 616.45 to 924.67 (C) 169 – 258 (D) 136 - 289
	678		Exercise 11.8xxvi		steam whirl stiffness = 89.44 kN/m.
Ch12
	689		Below Eqn. 12.8		Delete as shown below:
Ch13
	723		Example 13.4		Add in the end: From the construction, the measurement will be in clockwise so residual unbalance angle = From triangle OEA, let the angle OAE is f2, then we have or For , the measurement will be in clockwise so residual unbalance angle = .
	729		Example 13.5		From end 7^th line to be corrected as:
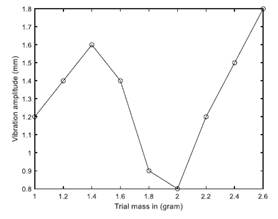
			Example 13.5 update all data		We have, influence coefficients as mm/kg a11 = 17.1542 +69.0116i mm/kg and mm/kg a12 = 1.1199e+02 - 1.0444e+01i mm/kg It is given that machine is symmetric about the centreline, hence Measurements, influence coefficients and correction mass are related as which can be simplified as with (mm/kg)^2 delta = -1.6901e+04 + 4.7070e+03i which gives the balancing mass and its angular position as wR = 0.3270 - 0.0762i kg wR_mag = 0.3358 kg wR_ang = -13.1223 deg. and wL = -0.2304 - 0.4165i kg wL_mag = 0.4760 kg wL_ang = -118.9496 deg.
	733		Below eqn. 13.31, replace x with c for mode shapes		For example, for simply supported boundary conditions, mode shapes are (i) I - mode : , (ii) II - mode : , and (iii) n^th- mode: .
	736		Eqn. 13.51 (use m1n and m2n)
	737		Equation 13.54		Second term has (z1):
	756		Exercise 13.2		Last line correct as “a necessary correction mass required”
	756		Exercise 13.5, Line 1		Add in the first line “…the influence coefficient method for Exercise 13.4.”
	758		Exercise 13.12		Let x be the amplitude difference with unit trial
	758		Exercise 13.13		Exercise 13.13 In the dynamic balancing of a rigid rotor by using the influence coefficient method, let the following measurement were made (i) and for a trial mass TR in the right plane and (ii) and for a trial mass TL in the left plane. Assume the measuring planes are “a” and “b”, trial mass (or balancing) planes are L and R, and αij is the influence coefficient with i = a, b and j = L, R. If WR and WL are the correction masses at the right and left planes, then prove that and
	758		Exercise 13.15		Exercise 13.15 In a simply supported rotor for flexible rotor balancing
	759		Exercise 13.16, Line 3		Delete as suggested the repeated sentence: Suggest whether dynamic balancing will be required. Suggest whether the dynamic balancing will be required?
Ch14
	784		Example 14.2		The horizontal load produces displacement of 10.3 μm and 3.3 μm in the horizontal and vertical directions respectively,
	784		Example 14.3 (update numbers)		As per solution
	817		Exercise 14.6 (in end add)		Take rotor speed equal to 2000 rpm
	817		Exercise 14.7		by the method of unbalance excitation (all measurement are done at 100 Hz speed), the following t
	817		Exercise 14.11(i)		C) taking measurements with different unbalance levels at a constant rotor speed
	818		Exercise 14.11(vii)		(C) when two orbits are elliptical and identical in shape (but not in size) and orientation.
Ch15	825		Para 2		Line 6: Amplitudes and phases of displacements, velocities Line 7: For acoustics three quantities are important: level, intensity, and power. Line 9: machine these parameters (vibrations and acoustics) and their analyses
	826		Para 2		For example, an instrument (for example, in thermometer (or voltmeter)) with a 30 cm (or 360°) scale would...
	827		Example 15.1		1. actual value of 1050–1000 = 50 rpm, 2. Hence, the tachometer could be used confidently to measure speed within ± (1040 × 0.096) = ±9.62 = ±10 rpm. 3. and absolute random error from mean of 0, 10, 10, 10 and 10 rpm
	828		Frequency range:		the accelerometer of n the order of 40 kHz.
	830		Below Eqn. (15.7),Line 2		“Equation (15.6)”
	833		Above Eqn. 15.8		The first natural frequency of a cantilever continuous beam is expressed as (refer Table 9.2)
	833		Example 15.3, last para		compared to the uncertainty. In one parameter, then should be compared to the uncertainty in one parameter, then
	834		Example 15.4		For L = 60 mm, from Equation 15.8, we have the lower upper bound of the natural frequency as Similarly, for L = 200 mm, we have the upper lower bound of the natural frequency
	841		-k(y2-y1)		Eqn. + sign to be replaced by – as
	856		Example 15.11 last lines		The output voltage is therefore E = {(3.557 /10)×10−3}(10−4 )= 3.557 ×10^−11 V should be The output voltage is therefore E = {(3.557 /10)×10−3}(10−4 )= 3.557 ×10^−8 V and  reduces to approximately 2.0 × 10^5 times should be reduces to approximately 178 times
	857		Exercise 15.6		Exercise 15.6: A small cantilever vibrometer is calibrated to obtain its characteristics by putting it on an engine, which is rotating at 500 ± 3.0 rpm. The measured length for resonance conditions is 7.2 cm ± 0.15 mm. Obtain the frequency that the measurement will show when L = 12 cm ± 0.4 mm. Also obtain the uncertainty in the measurement of frequency at this length. Obtain the phase angle for above conditions.
	858		Exercise 15.8		z = 0.72
	858		Exercise 15.8		Use Y instead of x? i.e., .
	858		Exercise 15.9		Use Y instead of x? that
	858		Exercise 15.9		changes in last line "1-" to be deleted: such that
	858		Exercise 15.10		seismic accelerometer is equal to the period of the maximum allowable
	858		Exercise 15.13		rad/s,
Ch16	887		Last para		Change last but one line "to a number of multiplications of the order of" to “to a number of multiplications to"
	888		First para		Fourth line: “which is only 2pN/N^2 = 2p/N of ...” to be changed to “so their ratio is only 2pN/N^2 = 2p/N of ...”
	924		Exercise 16.6xii		Windowing operations are performed on vibration signals to (A) to increase amplitude of main frequencies (B) reduce the leakage error (C) to decrease amplitude of spurious frequencies (D) all other three options
	924		Exercise 16.6xvi		D. Bisymmetrical
Ch17
	978		Exercise 17.3 viii		(D) 600 Hz Should be (D) 30 Hz
	928		section 17.1 1st para second line		and it is inherently inexistent. should be  and it is inherently in existent.
	935				bending moment with eight DOFs per node. Should be bending moment with eight DOFs per element.
	955		section 17.8 second paragraph last but 2 line		at tooth engagement, unbalance, ben shaft, worn/defective bearings, improper backlash, and poor should be bent shaft
	969				o TThe unbalanced sinusoidal voltage has should be The unbalanced sinusoidal voltage has o polyphaseinduction motor a should be polyphase induction motor a
	970		Figure 17.33
	972		Table 17.7		Short circuit freq. o for s = 0.0375  and s = 0.0375 in Harmonics index, k may be deleted o 81.5 Hz and 1.5 Hz (when i = 3 and n = 1), should be 81.5 Hz and 158.5 Hz (when i = 3 and n = 1),
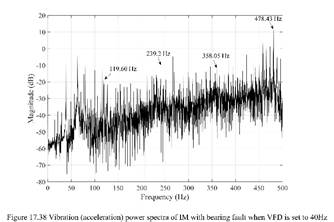
	972		Table 17.7		o Bearing failure 76.60 Hz and 159.6 should be Bearing failure... (refer Figure 17.39) 79.60 Hz and 159.6 o Bearing outer race fault characteristic vibration frequencies, fv, (Hz) should be Bearing outer race fault characteristic vibration frequencies, fv, (Hz) (refer Figure 17.38) o Short circuit frequency, fst (Hz) should be Short circuit frequency, fst (Hz) (refer Figure 17.37) o Broken bar frequency sidebands, fb (Hz)  should be Broken bar frequency sidebands, fb (Hz) (refer Figure 17.36)
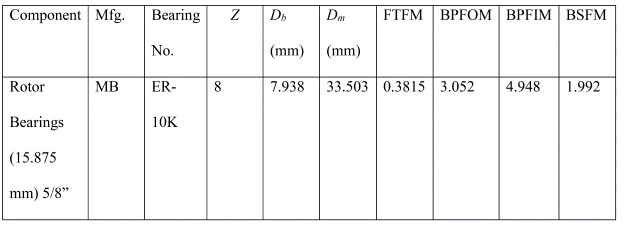
	972 and 974 (text)		Table 17.7		o Bearing fault case I calculated from f0 = 0.4nfr at 2341 rpm (39.02 Hz) of should be calculated from f0 = 0.4nfr at 2242.5 rpm (37.375 Hz) of o also in Table 17.7 fo = 0.4Zfr (Refer Table 17.2) at fr = 39.02 Hz (2341 rpm), Z = 8 should be fo = 0.4Zfr (Refer Table 17.2) at fr = 37.375 Hz (2242.5 rpm), Z = 8 also 0.4 × 8 × 39.02 = 119.60 Hz should be 0.4 × 8 × 37.375 = 119.60 Hz
	973				of pole pairs, i = 1, 3, 5, . . . , and n = 1, 2, . . ., (Gandhi et al., 2011). Change to: of pole pairs, the supply current harmonics, i = 1, 3, 5, . . . , and the side band harmonics, n = 1, 2, . . ., (Gandhi et al., 2011).
	975		Figure 17.38		FIGURE 17.38 y-axis is “Magnitude” (not “Stator current’)
Ch18	991		Above Figure 18.1		The angle is measured from the pole pair center line, Where a is the half of the angle subtend between a pair-pole, i.e. from the centre line of a pair-pole to one of the pole.
	991		Table 18.1		3-pole pairs at 45^o: 0.9659 4-pole pairs at 30^o and also at 60^o: 1.366
	992		Eqn. (18.1)		= = 0.707
	1008		Fig. 18.14		Check for positive sign of extreme left for sensor gain?
	1022		Eqn. (18.77)		It should be corrected as:
	1017		Example 18.1		1. Table 18.4 Area of core of pole-shoe magnet, 2.0´10^-4 2. In Eqn. (b): 3. Eqn. (c): ki =29.0245 N/A 4. Eqn. (d): kx=7.2561´10^4 N/m 5. Below eqn. (a) add: Where a is the half of the angle subtend between a pair-pole, i.e. from the centre line of a pair-pole to one of the pole.
	1050		Exercise 18.1		Replace: amplifier gain “”by””
	1050		Exercise 18.3(iii)		Magnetic bearings are	✔
	1052		Exercise 18.3(xix)		Corerd as:

Answers to Selected Problems

(please report if you find more solutions or errors: rtiwari@iitg.ac.in)

Chapter 2

Examples

2.1 8.8454´10⁴ to 1.1247´10⁵ N/m

2.2 156250 N/m

2.3 39240 N/m and 140.07 rad/s

2.4

2.5 2317.1 rad/s

2.6 29.45 and 289.23 rad/s

2.7 (i)

(ii)

(iii)

2.8 2.907.3 rad/s

2.9 191.87 rad/s

Exercises

2.1 ;

2.2 ,

, ;

for : is a complex quantity. The maximum feasible value of damping ratio for under-damped system will remain the same .

2.3 and

2.4 and

2.5 and(a)

(b) (c)

2.6 (pure translational motion); (pure rotational motion)

2.7 NA

2.8 NA

2.9 and

2.10

2.11

2.12

2.13

2.14

2.15 and

2.16 and

2.17 (a) coupled system

(b) coupled system and

2.18 and

2.19 ;

;

2.20 , .

2.21

2.22

2.23 M = I_d w² a

2.24 83.0 rad/s

2.25

(i) B (ii) C (iii) C (iv) C (v) D (vi) B (vii) C (viii) B (ix) D (x) B (xi) D (xii) B (xiii) D (xiv) B (xv) C (xvi) A (xvii) C (xviii) C (xix) D (xx) A (xxi) H (xxii) B (xxiii) B (xxiv) C (xxv) B (xxvi) C (xxvii) A (xxviii) D (xxix) A (xxx) C (xxxi) B]

Chapter 4

Examples

4.1 90.34 and 154.18 rad/s

4.2 (a) 11.81 and 66.94 rad/s (b) 11.81, 16.70, 66.94 and 94.66 rad/s

4.3 648.07, 748.33, 3240.40 and 3741.70 rad/s

4.4 7587.8 and 8908.2 rad/s

4.5 89.39, 187.64, 632.11 and 1326.80 rad/s

4.6 (a) 4530.9, 5393.9, 7840.4 and 9333.8 rad/s (b) 1289.0, 4654.0 and 17856.0 rad/s

Exercise

4.1 18.48 and 76.54 rad/s

4.2 90.34 and 154.18 rad/s

4.3 46.31 and 60.46 rad/s

4.4 46.31 and 60.46 rad/s

4.5

4.6 Refer Section 18.8 and Example 18.3

Equation of motion of the two offset discs rigid rotor-flexible bearings (can be written as

where the mass matrix M and the gyroscopic matrix G are

;

; ;

The stiffness and damping matrices of bearings are

The unbalance force vector is

The displacement vector is

4.7 Refer Chapter 3 and Exercise 4.6

Figure 1. (a) Displacement amplitude verses rotor spin speeds at bearing-1 (b) Displacement amplitude verses rotor spin speeds at bearing-2 (c) Displacement phase verses rotor spin speeds at bearing-1 (b) Displacement phase verses rotor spin speeds at bearing-2.

4.8 (i)

(ii)

(iii)

(iv)

(v)

4.9 153.6 and 2091.3 rad/s

4.10 5146.7 and 4383.8 rad/s

4.11 7658.3 and 8843.8 rad/s

4.12

4.13

4.14

4.15

4.16 14.1375 and 190.7494 rad/s

4.17 -

4.18 -

4.19 20.0 and 3170.9 rad/s

4.20

4.21

4.22

(i) D (ii) A (iii) D (iv) C (v) D (vi) D (vii) A

(viii) B (ix) C (x) D (xi) A (xii) D (xiii) C (xiv) D (xv) A (xvi) A (xvii) A (xviii) D (xix) A (xx) A (xxi) B

(xxii) B (xxiii) A (xxiv) E (xxv) A

Chapter 5

Examples

5.1 196.61 rad/s (point mass), 197.8628 rad/s (thin disc) and 393.2242 rad/s (very large disc)

5.2 (i) 842.81 rad/s (ii) 784.61 rad/s (iii) 23014.0 rad/s and (iv) 4.092.6 rad/s

5.3 Backward whirl natural frequency = 126.67 rad/s; Forward whirl natural frequency = 187.67 rad/s; Backward critical speed = 149.88 rad/s and Forward critical speed = 158.8794 rad/s.

5.4 Case I: without gyroscopic effect 29.455 and 289.23 rad/s

Case II: with gyroscopic effect 29.87 rad/s (F1), 29.03 rad/s (B1) and 169.41 rad/s (B2)

5.5 Case I: without gyroscopic effect 12983.0 rad/s and 6.8760.0 rad/s

Case II: with gyroscopic effect 14934.0 rad/s (F1), 11480.0 rad/s (B1)

and 44898.0 rad/s (B2)

5.6 Case I: without gyroscopic effect 90.34 rad/s

Case II: with gyroscopic effect 187.67 rad/s (F) and 126.67 rad/s (B)

Critical speeds 158.88 rad/s (F) and 149.88 rad/s (B)

Exercises

5.1 Case I: without gyroscopic effect 303.45 and 1255.20 rad/s

Case II: with gyroscopic effect 413.40 rad/s (F1), 241.78 rad/s (B1) and 909.56 rad/s (B2)

5.2 Case I: without gyroscopic effect 25.47 and 242.97 rad/s

Case II: with gyroscopic effect 27.01 rad/s (F1), 24.11 rad/s (B1) and 148.17 rad/s (B2)

5.3 Case I: without gyroscopic effect 26.82 and 122.26 rad/s

Case II: with gyroscopic effect 33.33 rad/s (F1), 22.50 rad/s (B1) and 84.16 rad/s (B2)

5.4 Refer Chapter 12

5.5

5.6 Case I: without gyroscopic effect 70.66 and 147.37 rad/s

Case II: with gyroscopic effect 84.76 rad/s (F1), 54.43 rad/s (B1) and 110.47 rad/s (B2)

5.7 -

5.8 108.47 rad/s (F) and 93.25 rad/s (B)

5.9 -

5.10 Refer Case II in Page 218

5.11 (i) 66.75 rad/s (ii) 66.47 rad/s (iii) 66.42 rad/s (iv) 66.54 rad/s

5.12 (i) (ii) - (iii)

5.13

5.14

5.15 1054.1 rad/s (F) and 953.46 rad/s (B)

5.16 -

5.17 -

5.18 Case I: without gyroscopic effect 25.47 and 242.97 rad/s

Case II: with gyroscopic effect 27.01 rad/s (F1), 24.11 rad/s (B1) and 148.17 rad/s (B2)

5.19 With gyroscopic effect 45.28 rad/s (F1), 41.45 rad/s (B1), 379.45 rad/s (F2) and 185.37 rad/s (B2)

5.20 Refer Equation (5.43)

5.21 -

5.22 d = 0.03374 m.

5.23 Natural whirl frequencies 32.50 rad/s (F) and 20.00 rad/s (B)

Critical speeds 27.26 rad/s (F) and 24.04 rad/s (B)

5.24 (refer Chapter 12)

5.25 d = 0.03615 m

5.26 3.9639´10⁵ N/m

5.27 Case I: without gyroscopic effect 191.45 and 428.09 rad/s

Case II: with gyroscopic effect 191.45 rad/s (F1), 191.45 rad/s (B1) and 247.16 rad/s (B2)

5.28

(i) B (ii) D (iii) A (iv) B (v) E (vi) A

(vii) B (viii) A (ix) B (x) B (xi) D (xii) B

(xiii) C (xiv) D (xv) D (xvi) A (xvii) B (xviii) A

(xix) A (xx) C (xxi) A (xxii) B (xxiii) A (xxiv) B

(xxv) B (xxvi) C (xxvii) D (xxviii) D (xxix) C (xxx) A

(xxxi) C (xxxii) A (xxxiii) B (xxxiv) A (xxxv) B (xxxvi) E

(xxxv) C

Chapter 6

Examples

6.1 22.3 Hz (Torsional), 9.9 Hz (Transverse)

6.2 0.00 and 257.43 rad/s

6.3 0.00 and 171.81 rad/s

6.4 0.00, 611.43 and 2325.23 rad/s

6.5 0.0, 611.4 and 2325.2 rad/s (same as Example 6.4)

6.6 0.00 and 9341.65 rad/s

6.7 233.88 rad/s

6.8 with

6.9 54.18 and 187.15 rad/s

6.10 0.00, 1373.75, 2453.40 and 3756.30 rad/s

6.11 0.00 and 142.22 rad/s

6.12 0.00, 142.12 and 382.78 rad/s

6.13 0.00, 924.39 and 1020.60 rad/s

6.14 0.00, 1610.31 and 4754.32 rad/s

Exercises

6.1 rad/s

6.2 rad/s

6.3 rad/s andrad/s

6.4 224.41, 1000.77 and 1706.11 rad/s

6.5 0.00, 320.77, 2323.41 and2704.91 rad/s

6.6 46.03 rad/s

6.7 (for assumed value: 0.00 and 76.38 rad/s)

6.8 0.00, 1273.41 and 12180.45 rad/s

6.9 0.00, 166.63 and 1994.67 rad/s

6.10 0.00, 146.16 and 6804.64 rad/s (Shaft A and arm have opposite motion)

6.11 0.00 and 97.49 rad/s

6.12 0.0334 m

6.13 3445.00 kg-m²

6.14 1008.90 and 1007.20 rad/s

6.15 441.65, 1323.95, 2259.90 and 5038.25 rad/s

6.16 491.19, 1150.85, 1709.51, 2346.71 and 5038.29 rad/s

6.17 0.00, 980.32, 1764.64, 2505.27 and 3756.59 rad/s

6.18 113.94 rad/s

6.19 478.74 and 918.98 rad/s

6.20 0.00, 469.00, 493.44, 1500.26, 1511.84, 2117.80 and 3936.12 rad/s

6.21 0.00, 302.68, 863.56, 1546.88, 1647.83, 2159.03, 2560.42, 3087.03, 3585.87, 4423.81, 5419.79, 6072.29 and 7149.01 rad/s

6.22 0.00, 202.28, 458.50 and 6336.98 rad/s

6.23 0.00 and 269.99 rad/s

6.24 0.00, 2108.19 and 2236.074219 rad/s

6.25 0.00, 188.13, 749.91 and 1055.81 rad/s

6.26 264.22 and 457.65 rad/s

6.27 364.054565 and 514.851685 rad/s

6.28 364.054565 and 514.851685 rad/s

6.29 202.72 and 782.02 rad/s

6.30 0.00, 347.30 and 456.064 rad/s

6.31 w_nf1 = 0,

[Answer: 6.32(i) A (ii) B (iii) D (iv) C (v) D (vi) D

(vii) D (viii) B (ix) C (x) A (xi) D (xii) A

(xiii) D (xiv) C (xv) D (xvi) A (xv) C (xvi) C

(xvii) D (xviii) C (xix) B (xx) D (xxi) A (xxii) B

(xxiii) D (xxiv) B (xxv) C (xxvi) D (xxvii) D (xxviii) C]

Chapter 7

Examples

7.1

7.2

7.3

with

7.4

w_nf1 = 0;

w_nf1 = 0.0; w_nf2 = 1089.7 rad/s.

7.5 w_nf1 = 233.9; w_nf2 = 27737.0 rad/s.

7.6 w_nf1 = 0.0; w_nf2 = 1116.0 rad/s; 3274.3 rad/s.

7.7 0.00; 3392.15; 7016.46; 11094.00; 15689.29; 20126.14 and 22188.01 rad/s

7.8 0.00; 142.13 and 382.77 rad/s

7.9 0.00; 928.05; 1010.95 and 3979.72 rad/s

Exercises

7.1 -

7.2

with

0.25; 3.17 6.30

7.3 -

7.4 -

7.5 0.00, 70.06 and 11094.50 rad/s

7.6 Refer to chapter 6 answers

7.7 (i) fixed-free: 1681.65, 5160.66, 8987.21, 13340.22, 18028.20 and 21632.72 rad/s

(ii) fixed-fixed: 3392.15, 7016.46, 11094.00, 15689.29 and 20126.14 rad/s

For both six elements.

7.8 (i) 320.66, 3423.80, 7032.75, 11104.74, 15696.04 and 20128.61 rad/s

(ii) 641.32, 7016.46, 7081.13, 15689.29 and 15716.23 rad/s

For both six elements

7.9 0.00, 158.95 and 5824.80 rad/s (epicylic gear ratio 2/7)

Similar as Exercise 6.10 but take gear ratio of epicylic gear train for speeds refer

above errata. “Speed of shaft A is 600 rpm and of the arm is 300 rpm with opposite

sense of rotation.”

7.10 316.08, 506.949 and 22195.971 rad/s

7.11 w_nf1 = 360.0 rad/s; w_nf2 = 13797.5 rad/s;

7.12 0.00, 1372.06, 2451.10, 3751.06, 36994.88 and 37059.86 rad/s

7.13 46.03 and 12314.83 rad/s

7.14 w_nf1 = 393.8 rad/s (with hole away from centre); w_nf2 = 396.1 rad/s (with hole at centre line).

7.15(a) C

Chapter 8

Examples (without shaft mass unless otherwise stated)

Example 8.1 w_nf1 = 29.4 rad/s; w_nf2 = 289.2 rad/s.

Example 8.2 w_nf1 = 2979.1 rad/s.

Example 8.3 w_nf1 = 266.6 rad/s; w_nf2 = 1303.7 rad/s.

Example 8.4 w_nf1 = 140.4 rad/s; w_nf2 = 908.5 rad/s; w_nf3 = 3209.3 rad/s; w_nf4 = 7436.8 rad/s.

Example 8.5 w_nf1 = 196.3 rad/s; w_nf2 = 6063.7 rad/s.

Example 8.6 w_nf1 = 29.5 rad/s; w_nf2 = 289.2 rad/s.

Example 8.7 w_nf1 = 168.4 rad/s; w_nf2 = 442.5 rad/s; w_nf3 = 1215.8 rad/s; w_nf4 = 1826.8 rad/s.

Example 8.8 w_nf1 = 214.6 rad/s; w_nf2 = 1076.6 rad/s; w_nf3 = 2469.7 rad/s; w_nf4 = 3846.5 rad/s.

Example 8.9 w_nf1 = 25.5 rad/s; w_nf2 = 243.0 rad/s.

Example 8.10 -

Example 8.11 w_nf1 = 261.2 rad/s.

Example 8.12 w_nf1 = 211.5 rad/s

Example 8.13 w_nf1 = 92.1 rad/s

Exercises (without shaft mass unless otherwise stated)

Exercise 8.1 w_nf1 = 84.6 rad/s; w_nf2 = 333.8 rad/s.

Exercise 8.2 w_nf1 = 4967.1 rad/s; w_nf2 = 30249.1 rad/s.

Exercise 8.3 w_nf1 = 4132.2 rad/s; w_nf2 = 19042.2 rad/s; w_nf3 = 40672.5 rad/s; w_nf4 = 55845.1 rad/s.

Exercise 8.4 w_nf1 = 25.5 rad/s; w_nf2 = 243.0 rad/s.

Exercise 8.5 Part I: w_nf1 = 28.0 rad/s; w_nf2 = 245.5 rad/s.

Part II: w_nf1 = 24.2 rad/s; w_nf2 = 175.6 rad/s.

Exercise 8.6 Part I: w_nf1 = 389.3 rad/s; w_nf2 = 1269.1 rad/s.

Part II: w_nf1 = 200.1 rad/s; w_nf2 = 489.4 rad/s; w_nf3 = 781.9 rad/s; w_nf4 = 1337.9 rad/s.

Exercise 8.7 w_nf1 = 158.2 rad/s; w_nf2 = 749.7 rad/s; w_nf3 = 1709.2 rad/s; w_nf4 = 2679.9 rad/s. w_nf5 = 3818.8 rad/s; w_nf6 = 6207.0 rad/s; w_nf7 = 7540.1 rad/s; w_nf8 = 9172.1 rad/s.

Exercise 8.8 w_nf1 = 1495.7 rad/s; w_nf2 = 3632.7 rad/s; w_nf3 = 4310.8 rad/s; w_nf4 = 5925.5 rad/s, w_nf5 = 8463.0 rad/s; w_nf6 = 9564.4 rad/s; w_nf7 = 174200.7 rad/s; w_nf8 = 349429.1 rad/s.

Exercise 8.9 w_nf1 = 60.4 rad/s; w_nf2 = 135.6 rad/s; w_nf3 = 991.7 rad/s; w_nf4 = 1765.1 rad/s.

Exercise 8.10 Refer Example 12.1

Exercise 8.11 w_nf1 = 0 rad/s; w_nf2 = 0 rad/s; w_nf3 = 319.6 rad/s; w_nf4 = 760.7 rad/s.

(Results are without shaft inertia and by FEM/TMM)

w_nf1 = 0 rad/s; w_nf2 = 0 rad/s; w_nf3 = 225.23 rad/s; w_nf4 = 577.07 rad/s.

(Results are with shaft inertia and by FEM)

Exercise 8.12 w_nf1 = 953.7 rad/s; w_nf2 = 2143.1 rad/s; w_nf3 = 2565.5 rad/s; w_nf4 = 3530.6 rad/s.

Exercise 8.13 w_nf1 = 45.0 rad/s.

Exercise 8.14 w_nf1 = 166.4 rad/s; w_nf2 = 455.4 rad/s.

Exercise 8.15 w_nf1 = 162.6 rad/s; w_nf2 = 446.1 rad/s; w_nf3 = 1309.2 rad/s; w_nf4 = 2006.3 rad/s; w_nf5 = 17819.3 rad/s; w_nf6 = 17906.9 rad/s.

Exercise 8.16 w_nf1 = 192.3 rad/s; w_nf2 = 979.9 rad/s; w_nf3 = 2151.9 rad/s; w_nf4 = 3334.2 rad/s, w_nf5 = 5062.5 rad/s; w_nf6 = 5451.5 rad/s; w_nf7 = 7806.6 rad/s; w_nf8 = 9268.9 rad/s.

Exercise 8.17 w_nf1 = 916.5 rad/s; w_nf2 = 5316.9 rad/s; w_nf3 = 9030.2 rad/s.

Exercise 8.18 w_nf1 = 1116.0 rad/s; w_nf2 = 8216.3 rad/s.

Exercise 8.19 142.7 rad/s; w_nf2 = 9129.7 rad/s.

Exercise 8.20 w_nf1 = 389.3 rad/s; w_nf2 = 1269.1 rad/s.

Exercise 8.21 w_nf1 = 0.0 rad/s; w_nf2 = 0.0 rad/s; w_nf3 = 245.2 rad/s; w_nf4 = 1456.4 rad/s.

(results are with shaft inertia and by FEM; also note the changes in the questions)

Exercise 8.22 -

Exercise 8.23 w_nf1 = 18074.4 rad/s; w_nf2 = 71720.4 rad/s. (without shaft mass)

Exercise 8.24 w_nf1 = 1156.7 rad/s; w_nf2 = 13043.6 rad/s.

Exercise 8.25 w_nf1 = 140.7 rad/s; w_nf2 = 212.7 rad/s.

Exercise 8.26 w_nf1 = 139.6 rad/s; w_nf2 = 1050.7 rad/s.

Exercise 8.27 w_nf1 = 185.4 rad/s; w_nf2 = 321.1 rad/s.

Exercise 8.28 w_nf1 = 0.0 rad/s; w_nf2 = 0.0 rad/s; w_nf3 = 69.5 rad/s

Exercise 8.29 Part I: w_nf1 = 0.0 rad/s; w_nf2 = 0.0 rad/s; w_nf3 = 306.1 rad/s; w_nf4 = 1331.7 rad/s

Part II: w_nf1 = 0.0 rad/s; w_nf2 = 0.0 rad/s; w_nf3 = 637.1 rad/s; w_nf4 = 1515.9 rad/s.

Exercise 8.30 w_nf1 = 631.8 rad/s; w_nf2 = 2039.0 rad/s.

Exercise 8.31

(i) A (ii) B (iii) B (iv) A (v) B

(vi) A (vii) B (viii) C (ix) A (x) B

(xi) D (xii) C

Chapter 9

Examples (with shaft mass unless otherwise stated)

Example 9.1

Example 9.2

Convergence study of natural frequencies (rad/sec)

Example 9.3 29.45 and 289.23 rad/s

Example 9.4 25.29, 234.87, 444.89 and 1667.94 rad/s

Example 9.5 1662.46, 3723.15, 4996.45, 5316.06, 6480.34, 9108.79, 174201.43 and

349418.31 rad/s

Example 9.6 116.17 , 438.40, 861.50, 1209.45, 1542.66, 2007.03, 6089.19, 7393.86

9301.39, 11637.67, 14839.49, 19807.60, 28112.42 and 29791.43 rad/s

Example 9.7 9.44, 46.16, 142.10 and 228.63 rad/s

Example 9.8 188.04, 239.62, 626.94, 791.67, 1321.47, 1652.78, 2210.31, 2641.42, 3115.19

3715.83, 4459.31, 5131.39, 7836.48, 8626.08, 9496.62, 10269.09, 11625.70

12999.24, 14284.97, 16518.14, 17894.79, 21018.27, 21796.76, 25053.46

29718.75, 30803.92, 34300.90 and 37076.63 rad/s

Example 9.9 Rayleigh coefficients a0 and a1 are 0.1897 and 0.0005

Damping matrix is

c =

0.6229 0.2959 -0.5648 0.2863

0.2959 0.1943 -0.2863 0.0958

-0.5648 -0.2863 0.6229 -0.2959

0.2863 0.0958 -0.2959 0.1943

Example 9.10 14.24 and 58.72 rad/s (with static condensation)

14.24, 57.57, 142.10, 264.22, 472.77 and 651.18 rad/s (without condensation)

Example 9.11 Natural frequencies before static condensation

wnf =

1.0e+05 *

Columns 1 through 12

0.0012, 0.0044, 0.0086, 0.0121, 0.0154, 0.0200, 0.0546, 0.0647, 0.0784, 0.0920

0.1039, 0.1160 rad/s

Columns 13 through 24

0.1278, 0.2336, 0.2551, 0.2852, 0.3190, 0.3543, 0.3915, 0.4266, 0.5911, 0.6504

0.7287, 0.8182 rad/s

Columns 25 through 28

0.9129, 0.9971, 1.2194, 1.2201 rad/s

Natural frequencies after static condensation

wnfs =

1.0e+04 *

Columns 1 through 12

0.0116, 0.0438, 0.0861, 0.1207, 0.1540, 0.2005, 0.5465, 0.6496, 0.7905, 0.9293

1.0456, 1.1622 rad/s

Columns 13 through 17

1.2800, 2.7647, 3.2783, 4.1075, 5.1230 rad/s

Example 9.12 Natural frequencies before dynamic condensation

wnfd =

14.3455 and 58.0192 rad/s

Natural frequencies after dynamic condensation

wnf =

14.2368, 57.5735, 142.0996, 264.2237, 472.7740 and 651.1824 rad/s

Exercises (results shows for minimum number of elements and with shaft mass unless otherwise stated)

Exercise 9.1 w_nf1 = 27.8 rad/s; w_nf2 = 241.2 rad/s; w_nf3 = 966.4 rad/s;

Exercise 9.2 w_nf1 = 437.4 rad/s; w_nf2 = 2699.3 rad/s; w_nf3 = 9927.9 rad/s; w_nf4 = 25526.0 rad/s.

Exercise 9.3 w_nf1 = 28.4 rad/s; w_nf2 = 736.4 rad/s; w_nf3 = 2675.7 rad/s; w_nf4 = 10691.8 rad/s.

Exercise 9.4 w_nf1 = 27.8 rad/s; w_nf2 = 241.2 rad/s; w_nf3 = 966.4 rad/s

Exercise 9.5 w_nf1 = 84.4 rad/s; w_nf2 = 330.6 rad/s; w_nf3 = 7413.5 rad/s; w_nf4 = 26629.0 rad/s.

Exercise 9.6 With shaft mass (two elements)

w_nf1 = 436.1 rad/s; w_nf2 = 2643.5 rad/s; w_nf3 = 8427.8 rad/s; w_nf4 = 16446.3 rad/s.

Without shaft mass

w_nf1 = 738.8 rad/s; w_nf2 = 5113.8 rad/s; w_nf3 = 15662.4 rad/s; w_nf4 = 26492.6 rad/s.

Exercise 9.7 Part I: w_nf1 = 25.3 rad/s; w_nf2 = 234.9 rad/s; w_nf3 = 444.9 rad/s; w_nf4 = 1667.9 rad/s.

Part II: w_nf1 = 24.0 rad/s; w_nf2 = 146.0 rad/s; w_nf3 = 297.7 rad/s; w_nf4 = 792.2 rad/s.

Exercise 9.8 For D₁D₂ = 0.75.

With FEM with shaft mass, natural frequencies are (3 elements)

w_nf1 = 199.9 rad/s; w_nf2 = 489.4 rad/s; w_nf3 = 779.8 rad/s; w_nf4 = 1334.0 rad/s.

With FEM without shaft mass, natural frequencies are (3 elements)

w_nf1 = 200.1 rad/s; w_nf2 = 489.4 rad/s; w_nf3 = 781.9 rad/s; w_nf4 = 1337.9 rad/s.

Exercise 9.10 w_nf1 = 3.9 rad/s; w_nf2 = 28.7 rad/s; w_nf3 = 74.0 rad/s; w_nf4 = 182.0 rad/s.

Exercise 9.11 w_nf1 = 916.5 rad/s; w_nf2 = 5316.9 rad/s; w_nf3 = 9030.2 rad/s.

Exercise 9.12 b = c = 0.7 m (number of elements 3)

w_nf1 = 16.2 rad/s; w_nf2 = 37.7 rad/s; w_nf3 = 204.8 rad/s; w_nf4 = 248.6rad/s,

w_nf5 = 600.8 rad/s; w_nf6 = 1020.9 rad/s.

Exercise 9.13 1st backward 6400 rpm and 1st forward 11800 rpm,

2nd backward 12600 rpm and 2nd forward 17600 rpm.

Exercise 9.14 w_nf1 = 167.79 rad/s; w_nf2 = 316.12 rad/s

Exercise 9.15 w_nf1 = 59.3 rad/s; w_nf2 = 112.5 rad/s; w_nf3 = 2.187.1 rad/s; w_nf4 = 2196.7 rad/s w_nf5 = 9167.9 rad/s.

Exercise 9.16 w_nf1 = 89.4 Hz (562.0 rad/s)

Exercise 9.17 w_nf1 = 4.4 rad/s; w_nf2 = 79.3 rad/s; w_nf3 = 106.6 rad/s; w_nf4 = 285.9 rad/s

Exercise 9.18

Exercise 9.19

Exercise 9.20 w_nf1 = 5.7 rad/s; w_nf2 = 9.8 rad/s; w_nf3 = 2866.6 rad/s; w_nf4 = 8279.9 rad/s

Exercise 9.21

(i) A (ii) C (iii) B (iv) A (v) B (vi) A (vii) A (viii) A (ix) C (x) C (xi) C

Chapter 10

Examples

Chapter 11

Examples

Example 11.1 Eccentricity ratio 0.2

Example 11.2 Stable

Determinants

D1 = 7.4600e+12, D2 = 4.4043e+23, D3 = 1.3199e+30, D4 = .2998e+31

First column Routh table

a4 = 25, a3 = 3e6, b3 = 5.9113e+10, c3 = 7.4429e+12, d3 = 3.3750e+14

Example 11.3 Stable

Determinants

D1 = 2.07e12, D2 = 3.623596e22, D3 = 7.247192e28, D4 = 1.80912e30

First column Routh table

a4 = 25, a3 = 2e6, a2 = 1.7518e10, a1 = 2.07e12, a0 = 1.315e13

Example 11.4 Oil –whip frequency 1990 rad/s, zeta = 0.1, wnfd = 1.9900e+03

Example 11.5 128.4265 rad/s

Example 11.6 -

Example 11.7 Unstable speed range due to asymmetry in shaft is 42.4682 rad/s to 47.1869 rad/s

Unstable speed range due to unbalance is 21.2341 rad/s to 23.5935 rad/s

Example 11.8 The lower and upper instability ranges at different modes are

wn1_L =

1.0e+05 *

0.0103, 0.0416, 0.0958, 0.1764, 0.2894, 0.4457, 0.6658, 0.9948, 1.5616, 3.0547

wn1_U =

1.0e+05 *

0.0145, 0.0588, 0.1355, 0.2494, 0.4093, 0.6303, 0.9415, 1.4069, 2.2085, 4.3200

wn2_L =

1.0e+09 *

0.0004, 0.0061, 0.0312, 0.0998, 0.2467, 0.5164, 0.9594, 1.6258, 2.5570, 0.9692

wn2_U =

1.0e+10 *

-0.0001, -0.0013, -0.0064, -0.0192, -0.0442, -0.0846, -0.1421, -0.2157, -0.3034, 1.4097

wn3_L =

1.0e+05 *

0.0102, 0.0408, 0.0919, 0.1634, 0.2553, 0.3676, 0.5003, 0.6535, 0.8271, 1.0211

wn3_U =

1.0e+05 *

0.0144, 0.0578, 0.1300, 0.2310, 0.3610, 0.5198, 0.7076, 0.9242, 1.1697, 1.4440

Example 11.9

(i)

(ii)

(iii)

Example 11.10

Exercises

Exercise 11.1 -

Exercise 11.2 Refer Section 11.8.

Exercise 11.3

Equations of motion

Eigen value problem (homogeneous equations)

Characteristic equation

Exercise 11.4 (i) whirl frequency as 44.7743 rad/s, unstable (ii) whirl frequency as 44.7186 rad/s, stable.

For boundary of stability (BOS) whirl frequency will be same as undamped natural frequency and given by ω_nf = 44.72 rad/s.

Hint: Equate Eqns. 11.214 and 11.215 and try to obtain feasible expression of alpha

and beta. In Eqn. 11.215, if alpha is negative system will be stable. Beta gives

whirl frequency.

Exercise 11.5 Stable

Determinants

D1 = 67.07e+009, D2 = 38.03e+018, D3 = 41.07e+021, D4 = 9.24e+018

First column Routh table

a0 = 426.06e+009, a1 = 67.07e+009, a2 = 567.01e+006, a3 = 1.08e+003

a4 = 225.00e-006, a5 = 0.00e+000, a6 = 0.00e+000, a7 = 0.00e+000

Exercise 11.6

Exercise 11.7

Exercise 11.8

(i) C	(ii) A	(iii) D	(iv) B	(v) B	(vi) C	(vii) C	(viii) A	(ix) B	(x) A
(xi) C	(xii) A	(xiii) B	(xiv) C	(xv) A	(xvi) C	(xvii) B	(xviii) C	(xix) B	(xx) D
(xxi) A	(xxii) D	(xxiii) B	(xxiv) A	(xxv) A	(xxvi) A	(xxvii) C	(xxviii) C	(xxix) D	(xxx) C
(xxxi) A	(xxxii) B	(xxxiii) B	(xxxiv) B	(xxxv) A	(xxxvi) D	(xxxvii) D	(xxxviii) D	(xxxix) B	(xxxx) B
(xxxxi) C

Chapter 12

Examples

Ex

Chapter 13

Examples

Example 13.1 (a) Resultant unbalance and resultant unbalance moment are

(b) Equivalent unbalances are

(c) equivalent an unbalance and a couple

Example 13.2

The location of the angular position is 180^o and the magnitude of the unbalance mass is 2.0 gm.

Example 13.3

Example 13.4 x = 5.1478, m_unb = 0.0058 and angle = 307.4^o

Example 13.5 wR_mag = 0.3358 kf, wR_ang = -13.1^o

wL_mag = 0.4760 kg, wL_ang = -119.0^o

Example 13.6 -

Example 13.7 -

Exercises

13.1 m_unb gm Ð 314.4^o.

13.2 m_unb = 6.5271 gm Ð 257.3 deg.

13.3 and

and

% Change in W_R = 20.1 and % Change in W_L = 10.2.

13.4 and

13.5 W_R = 18.4522 gm Ð -138.8^o, % Change in Wr = 73.5;

W_L = 21.2117 gm Ð 118.9^o % Change in W_L 47.5

13.6 -

13.7 -

13.8 -

13.9 (i) and (ii) and

(iii) and

(iv) and

(v) and

(vi) and for n = 1, 3, 5, …and for n =2, 4, 6, ….

13.10 -

13.11 -

13.12 -

13.13 -

13.14

13.15

13.16 Resultant force magnitude, its phase are and , respectively, with .

This angle will be CCW from y-axis while looking along the z-axis. That means from x-axis. The resultant force R₂ will be same as R₁ also its phase magnitude will be same as . But its direction will be obtained as

Forces: along positive x-axis and force P_y2 along negative y-axis

The resultant force R₂ will be act from y-axis in CCW while looking along z-axis.

13.17 m₁₂ = m₁₂ = m₂₂ = 0

13.18 (i) (ii)

13.19

13.20 Balancing mass 1.2826 gm at – 22.63^o and at a radius of 6 cm.

13.21 gm

13.22

13.23 Plane 1: mass 332.5001 gm at 28.92^o and Plane 2: mass 188.4042 gm at ̶ 28.78^o (or 331.22^o)

13.24 -

13.25

(i) D	(ii) C	(iii) A	(iv) D	(v) B	(vi) B	(vii) A	(viii) B	(ix) C	(x) B
(xi) C	(xii) C	(xiii) A	(xiv) D	(xv) A	(xvi) A	(xvii) C	(xviii) B	(xix) C	(xx) D
(xxi) C	xxii B	xxiii C	xxiv D	xxv B	xxvi D	xxvii C	xxviii A	xxix B	xxx A

Chapter 14

Examples

Example 14.1 360 N

Example 14.2

Example 14.3

Example 14.4

Example 14.5 -

Example 14.6 MN/m; MN/m; MN/m; N/m

kN-s/m; kN-s/m; kN-s/m; kN-s/m

Example 14.7 -

Exercises

Exercise 14.1 MN/m

Exercise 14.2 MN/m

Exercise 14.3

Exercise 14.4 -

Exercise 14.5

Exercise 14.6 N/m ;

Exercise 14.7 Case I: Nan

Case II

Exercise 14.8

Exercise 14.9

Exercise 14.10

Exercise 14.11

(i) D	(ii) B	(iii) A	(iv) D	(v) D	(vi) D	(vii) D	(viii) A	(ix) A	(x) B
(xi) D	(xii) A	(xiii) A	(xiv) C

Chapter 15

Examples

Example 15.1 Precision = 1% (± 10 rpm), percentage accuracy = 5 %, and standard deviation = 8.94 rpm

Example 15.2 Case I: 2.24 % Case II: 1.41 %

Example 15.3 1.49 %

Example 15.4 1 %

Example 15.5 2.4285

Example 15.6 0.412

Example 15.7 210.82 rad/s

Example 15.8 11.18 kN (or 12 kN)

Example 15.9 53.0103 dB

Example 15.10 81.5113 dB

Example 15.11 3.5566e-08 V

Exercise Problem Final Answers:

Exercise 15.1

Exercise 15.2

Exercise 15.3

Exercise 15.4 V, W; V , W;

V, W

Exercise 15.5 cm ; cm

Exercise 15.6 rad/s and rad/s

Exercise 15.7 s,

Exercise 15.8

Exercise 15.9 m/s²

Exercise 15.10 dB

Exercise 15.11 Y₁ = 1.5268´10^-5m

Exercise 15.12 N/m, kg

Exercise 15.13 rad/s

Exercise 15.14 X = 0.0067 mm, a = 3.0000 m/s²

Exercise 15.15

Exercise 15.16 rad/s

Exercise 15.17

(i) D	(ii) D	(iii) B	(iv) C	(v) A	(vi) B	(vii) C	(viii) C	(ix) A	(x) C
(xi) B	(xii) A	(xiii) B	(xiv) B	(xv) B	(xvi) C	(xvii) A	(xviii) D	(xix) A	(xx) C
(xxi) B	(xxii) D	(xxiii) C	(xxiv) A	(xxv) C	(xxvi) D	(xxvii) A	(xxviii) B	(xxix) B	(xxx) C
(xxxi) D	(xxxii) C	(xxxiii) D	(xxxiv) C	(xxxv) C	(xxxvi) B	(xxxvii) B	(xxxviii) B	(xxxix) C	(xxxx) A

Chapter 16

Examples

Example 16.1 Correct frequencies 120 and 460 Hz

Missed with spurious frequency 200 Hz

Spurious frequencies 100 and 300 Hz

Example 16.2 (i) stationary 1×30, (ii) stationary 2×30,

(iii) 25 – 30 = - 5 Hz in the opposite direction as the actual shaft rotation,

(iv) 34 – 30 = 4 Hz in the same direction as the actual shaft rotation,

(v) 54 - 2×30 = - 6 Hz in the opposite direction as the actual shaft rotation,

(vi) 76 – 2×30 = 16 Hz or 76- 3×30 = - 14 Hz; we will see the minimum of these two, i.e. 14 Hz in the opposite direction as the actual shaft rotation,

(vii) stationary 20×30,

(viii) 15 -30 = - 15 Hz, since it is half the frequency of the shaft if we mark two different colours on the diagonally opposite on the shaft surface we will see them alternatively,

(ix) 45-30 = 15 Hz, in this case also if we mark two different colours on the diagonally opposite we will see them in alternatively,

(x) 13- 30 = - 17 Hz in the opposite direction as the actual shaft rotation, and (xi) 18 -30 = -12 Hz, in the opposite direction as the actual shaft rotation.

Example 16.3

Example 16.4

Example 16.5

Example 16.6

Example 16.7

Example 16.8

Example 16.9 So 1×, -1×, 2×, -2×, 3×, -3× , 4× and -4× harmonics have respectively amplitude 3.5, 1.5, 3.5, 0.5, 3.0, -4.0, 2.5, 4.5. It indicate that all harmonics except -3× have the same zero phase. The - 3× harmonics has 1800 phase.

Exercises

Exercise 16.1 (i) Up to 250 Hz there will not be aliasing effect. (ii) Sampling interval 0.000667 s

Exercise 16.2 X₀ = 4.0000 + 0.0000i; X₁ = -0.7225 - 0.3479i;

X₂ = -1.4010 - 1.7568i X₃ = 0.1235 + 0.5410i

X₄ = 0.1235 - 0.5410i X₅ = -1.4010 + 1.7568i

X₆ = -0.7225 + 0.3479i

Exercise 16.3

(i) The sampling frequency is 175 Hz that gives the Nyquist frequency as 175/2 =87.5 Hz. That means 25 Hz and 40 Hz will be corrected captured. However, corresponding to 100 Hz there will be a spurious signal of frequency 100 – 87.5 = 12.5 Hz.

(ii) The frequency of signal to be captured is 3 kHz, so sampling frequency should be twice of it that is f_s = 6 kHz. So the sampling interval will be Dt = 1/ f_s = 1/6000 = 1.667´10^-4 sec. For T = 1 second data, the number of points will be N = T/Dt = 1/(1.667´10^-4) = 6000.

(iii) The leakage error can be minimized by (a) tuning the sample length so that signal is captured for its multiple period for this case no leakage error will be present, (b) windowing function, however, for this case the amplitudes will not be to the scale, it will be scaled down.

(iv) X₀ = 0.0000 + 0.0000i; X₂ = 0.2000 + 0.2000i

X₃ = 0.0000 + 0.0000i X₄ = 0.2000 - 0.2000i

Exercise 16.4

Exercise 16.5 (i) Given that

;

Now, Fundamental frequency is given as

The Nyquist frequency is given as

Now, to measure 1 kHz signal, we should have sampling interval as

With sampling frequency of 2 kHz.

(ii) -

Exercise 16.6

Answers: (i) B (ii) A (iii) A (iv) B (v) B (vi) B (vii) D (viii) B (ix) D (x) A (xi) D (xii) B

(xiii) D (xiv) C (xv) B (xvi) C (xvii) C

(xviii) A (xix) C (xx) C (xxi) A (xxii) C (xxiii) A

(xxiv) D (xxv) D (xxvi) A (xxvii) B (xxviii) D (xxix) B

(xxx) D (xxxi) C (xxxii) C (xxxiii) C (xxxiv) D (xxxv) C

(xxxvi) A (xxxvii) A (xxxviii) B (xxxix) D (xxxx) C (xxxxi) B

Chapter 17

Examples

Example 17.1

Example 17.2

Bearing specifications and fault frequency multipliers

Exercises

Exercise 17.1

Calculations of Possible Excitation Frequencies

Due to the Angular Speed of Conveyor Belt Rollers & its Bearings: The conveyor belt is supported by rollers and it is assumed that there is no skidding of belt over rollers (it will be ensured when belt has prescribed pretension and rollers are not damaged). This allows us to calculate the angular speed of rollers, f_R, (or idler passing frequency) as

Hz (1)

where = 4.2 m/s is the speed of the conveyor belt (or the circumferential velocity of the roller of the conveyor belt) and = 159 mm is the outer diameter of roller.

The fundamental ball-pass (or train or cage) frequency for a deep-groove ball bearing of the conveyor belt roller, when the outer ring (i.e., the belt roller) of the roller is rotating with , is given as

(2)

where D_b = 11.1 mm and D_m = 43.5 mm are the ball and pitch diameters of the bearing. When there is a fault in a bearing, then only this frequency would be of any significance.

Due to the Linear Speed of Conveyors: The frequency of passing the carrying belt (or belt passing frequency over the roller supports) can be calculated as

Hz (3)

where is the time period of conveyor belt over two roller spans, is the roller support span for the carrying belt i.e. the distance between two roller supports for the belt, and is the speed of the conveyor belt. For the present case, the roller support span had two values (a) L_cb = 22.5/6 = 3.75 m for the carrying belt (since it has six roller supports in one gallery), and (b) L_rb = 22.5/3 = 7.5 m for the return belt (since it has three roller supports in one gallery). For 25m span between two neighbouring rollers the frequency would go down to 1 Hz. Similarly, for the returning belt, the belt passing frequency can be obtained as

Hz (4)

Another passing frequency of the belt through a single gallery could be obtained as

Hz (5)

It should be observed that excitation frequencies related to belt are very low (below 2 Hz) and the major force which comes all the time to the gallery structure is due to belt movement only. Hence, these frequencies and their few higher harmonics (2×, 3×, etc.) would be very dangerous if some of the natural frequencies of gallery structure are present in these low frequency reasons.

During to the Start-up of the Conveyor Belt System: It was observed that during start-up of conveyor belt system from the rest gave a low frequency and high amplitude vibrations. However, it stabilised as soon as conveyor reached its maximum speed and loading. Some transient vibration spectrum of this sort was captured and will be presented and discussed in the subsequent section.

Due to Engines of the Inspection Vehicle: The inspection vehicle engine (2600 rpm) that runs on galleries itself to carry maintenance personal of conveyor belt could be a source of excitation with a frequency of

Hz (6)

and the inspection vehicle itself could be another source of vibration especially during sudden starting and stopping of the vehicle, which could excite several frequencies. The generator on the inspection car could be a source of vibration (3600 rpm = 60 Hz). However, these forces are occasional on the structure.

Due to Winds and Earth Quakes: Apart from these some unexpected forces such as wind (gust) forces and earth quakes are additional unknown forces that could damage the structure. These are exceptional cases; however, some preventive measure would definitely be increasing the life of the structure.

Among all these frequencies the forces due to conveyor belt linear motion is expected to have a predominant effect on the vibration of steel gallery structures due to possible resonance conditions, especially of the fundamental frequency and few higher natural frequencies. This is due to the presence of a major dynamic force in the gallery towards movement of the about 34 km long massive belt with lime stones on it.

Exercise 17.2 -

Exercise 17.3

(i) C	(ii) D	(iii) A	(iv) D	(v) C	(vi) B	(vii) C	(viii) D	(ix) A	(x) A
(xi) B	(xii) C	(xiii) D	(xiv) B	(xv) D	(xvi) D	(xvii) B	(xviii) D	(xix) C	(xx) B
(xxi) D	(xxii) C

Chapter 18

Examples